穿越中国各省的最短路径问题

发表于
| 本文字数： 3.7k

如果我们想要穿越中国所有的一级行政区并最终返回起始位置，满足条件的最短路径会是什么呢？这看起来类似旅行推销员问题（ TSP ），但要复杂不少。在TSP里每个城市都简化为了一个点，而在这里每个行政区的面积是非零的，点可以在区域内任意游走。

为了找到全局最优解，可以使用模拟退火、遗传算法这类全局优化算法。对于只要求经过所有省份但最终不需要返回原点的情形，这个知乎回答给出了一个模拟退火的解法。这里我借鉴了此方法来解闭合路径的情形（但具体的实现细节与用的参数有些不同），得到的最短路程是9818km。

所有一级行政区（包括港澳台）的地图数据源于Mathematica：

1
regions=CountryData["China","AdministrativeDivisions"]~Join~(CountryData/@{"HongKong","Macau","Taiwan"})

先考虑不回到出发地的情形，正好可以对照上面提到的这个回答，用来验证算法和调参的效果。我得到的最短路程7637km和他得到的7649km基本上是一样的。当然要是看具体路径的话还是有点差别的。

模拟退火的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
RandomLocation[reg_] := 
  reg["Polygon"] /. GeoPosition -> Identity // RegionBoundary // RandomPoint // GeoPosition

NewLocs[locs_, regs_] := 
  Module[{newLocs = locs, i = RandomInteger[{1, Length[regs]}]},
    newLocs[[i]] = RandomLocation[regs[[i]]]; newLocs]

RegionIdx[name_] := 
  Position[regions, _?(StringStartsQ[#["Name"], name] &)] // First // First;

FindBestPath[locs_] := 
  FindShortestTour[locs, RegionIdx["Heilongjiang"], RegionIdx["Xizang"]];

OptimizePath[regs_, findPath_, initLocs_, initT_, Tmin_, coolingRate_, nsteps_] :=
  Module[{bestLocs, bestLen, bestOrder, currLocs = initLocs, currLen, currOrder,
    tryLocs, tryLen, tryOrder, T = initT, n, currStep = 1},
    {currLen, currOrder} = findPath[currLocs];
    bestLen = currLen;
    Do[
      tryLocs = NewLocs[currLocs, regs];
      {tryLen, tryOrder} = findPath[tryLocs];
      If[RandomReal[] < Exp[-QuantityMagnitude[tryLen - currLen, "Kilometers"]/ T],
        {currLocs, currLen, currOrder} = {tryLocs, tryLen, tryOrder};
        T = Max[T*coolingRate, Tmin]; currStep = n];
      If[currLen < bestLen, {bestLocs, bestLen, bestOrder} = {currLocs, currLen, currOrder}];
      If[n - currStep > 50, T *= 2], {n, nsteps}
    ];
    Print[UnitConvert[bestLen, "Kilometers"]];
    {bestLocs, bestLen, bestOrder}
  ]

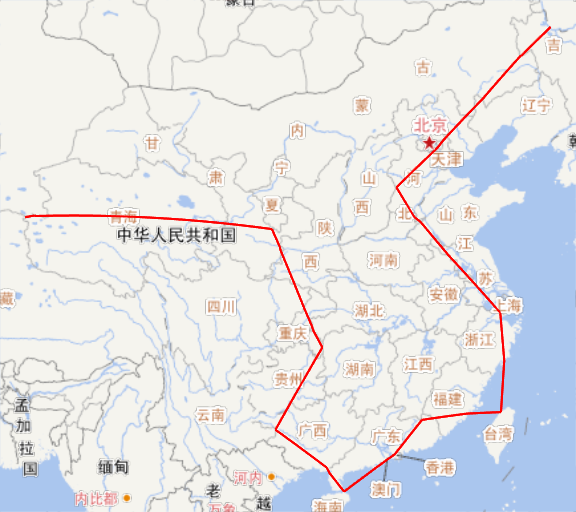
验证了算法，然后就可以开始算最短的闭合路径了。我试了10次，每次初始温度initT = 100、最低温度Tmin = 1、冷却率coolingRate = 0.99，共跑10000步，最短的一次结果是9834km。

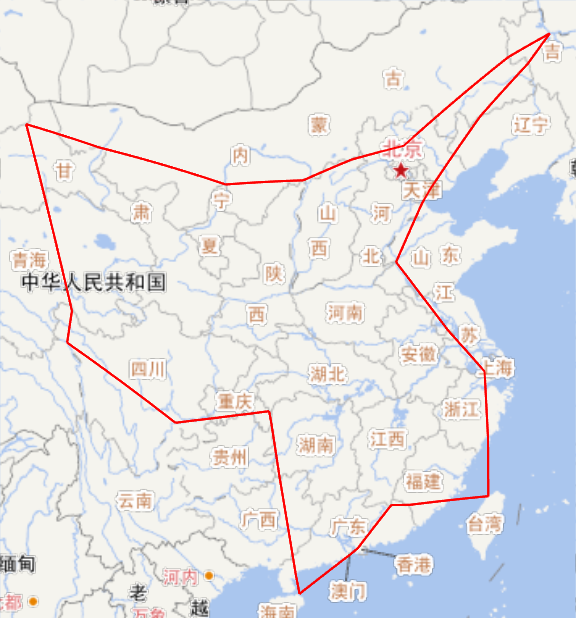
仔细看上图，可以发现路径在川青边界上折了一下，显然不是最优的。所以我试着降低了模拟退火的温度又跑了一会，这下就降到了9818km。

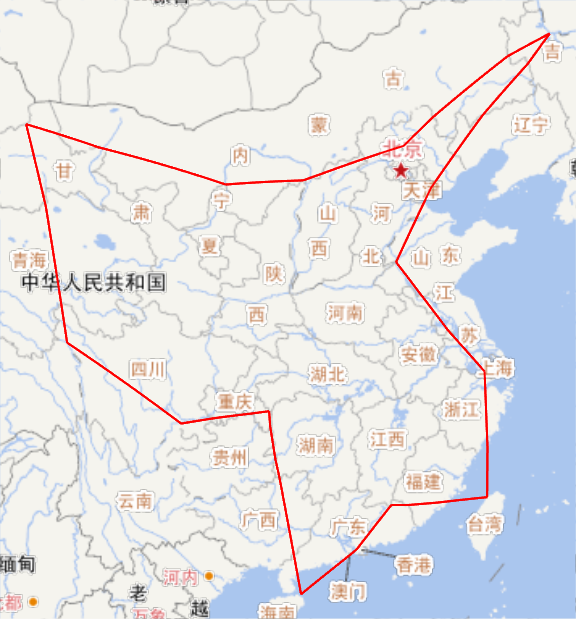
顺便提一下，上面使用的台湾地图数据没有包括离岛的澎湖，所以我尝试把台湾本岛上的点改到澎湖，不过路程并没有缩短，反而略微增加了一点。

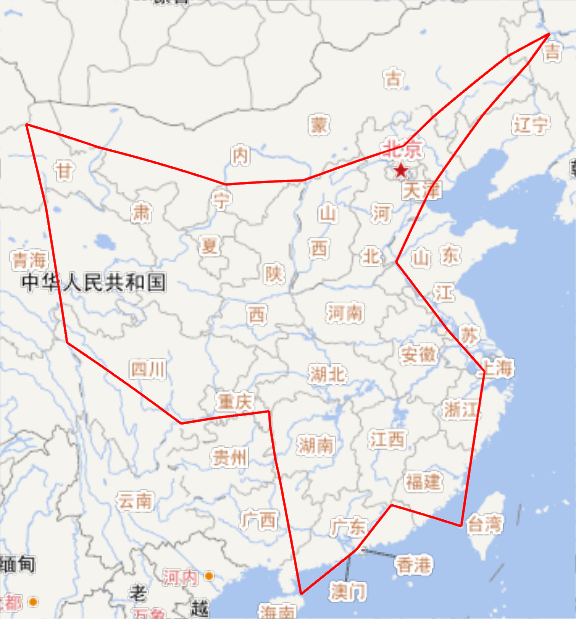
另外，我还以得到的最短路径为基础，算了下开车或者步行所需的路程和时间。本来是想用Mathematica里现成的 TravelDirections、TravelDistance 等函数进行旅程计算的，但我实测发现这功能至少在中国很不好用，常常会找不到路径，所以最后改用了Google Maps的API。其中，使用了这里的代码将Google Maps返回的路径解码，其他部分如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
TravelData[pts_,mode_] :=
  Import["http://maps.googleapis.com/maps/api/directions/json?origin="<>pts[[1]]<>
    "&destination="<>pts[[-1]]<>"&waypoints="<>StringRiffle[pts[[2;;-2]],"|"]<>
    "&mode="<>mode<>"&sensor=false","RawJSON"];

GoogleMapPath[locs_,mode_:"driving"] :=
  Module[{pts,travelData,encodedPaths,path,len,time},
    pts = StringRiffle[#/.GeoPosition->Identity,","]&/@locs;
    travelData = TravelData[#,mode]&/@Partition[pts~Join~{pts[[1]]},UpTo[10],9];
    encodedPaths = #[["routes",1,"overview_polyline","points"]]&/@travelData;
    path = GeoPosition/@Reverse/@(Join@@(DecodePolyline[#]&/@encodedPaths));
    len = Quantity[#[["routes",1,"legs",All,"distance","value"]]&/@travelData//Flatten//Total,"Meters"];
    time = Quantity[#[["routes",1,"legs",All,"duration","value"]]&/@travelData//Flatten//Total,"Seconds"];
    {path,len,time}]

{drivingPath,drivingLen,drivingTime}=GoogleMapPath[locs4];

{walkingPath,walkingLen,walkingTime}=GoogleMapPath[locs4,"walking"];

当然开车或步行是没法去台湾的，所以这里的路径就没有考虑台湾。最终的结果见下面两张图，开车总里程近1.37万公里，需要近8天。步行的话总里程近1.3万公里，需要差不多四个月才能走完。

开车路径
步行路径

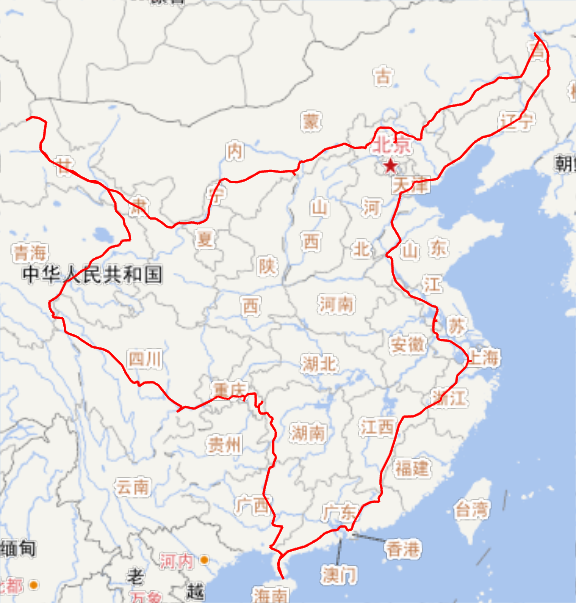
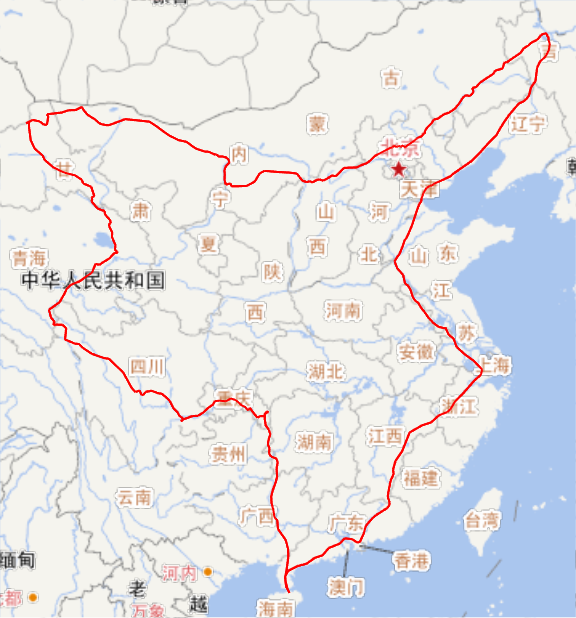
代码我放到了Wolfram Cloud上，有兴趣的同学可以戳这里。

注：本文首发于知乎问题 如果有人想走遍中国所有的省级行政区（含港澳台），并回到出发地，总路程最小可以是多长？