主成分分析(PCA)是数据降维最经典的方法之一了,不过只能局限于线性降维。最近在学校的数据挖掘课上学到了对PCA基于核技巧(kernel trick)的非线性扩展——核PCA,就顺便翻译了相应的英文维基百科条目。核函数可能在支持向量机、高斯过程等机器学习算法中更常见,不过所有核方法的基本思想都是一致的,就是用核函数将数据非线性映射到高维空间中,再用线性方法处理就好了。
核主成分分析 (kernel principal component analysis,简称kernel PCA)是多变量统计领域中的一种分析方法,是使用核方法对主成分分析的非线性扩展,即将原数据通过核映射到再生核希尔伯特空间后再使用原本线性的主成分分析。
背景:线性主成分分析
线性PCA对于中心化后的数据进行分析,即 $$\frac{1}{N}\sum_{i=1}^N \mathbf{x}_i = \mathbf{0},$$
其中 $\mathbf{x}_i$ 是 $N$ 个多变量样本之一。之后将协方差矩阵 $$C=\frac{1}{N}\sum_{i=1}^N \mathbf{x}_i\mathbf{x}_i^\top$$
对角化。换言之,即是对协方差矩阵进行特征分解 $$\lambda \mathbf{v}=C\mathbf{v}$$
或写作 $$\lambda \mathbf{x}_i^\top \mathbf{v}=\mathbf{x}_i^\top C\mathbf{v} \quad\forall i\in [1,N].$$
引入核方法
一般而言,$N$ 个数据点在 $d \geq N$ 维空间中是线性不可分的,但它们在 $d \geq N$ 维空间中则是几乎必然线性可分的。这也意味着,如果我们能将 $N$ 个数据点 $\mathbf{x}_i$ 映射到一个 $N$ 维空间 $$\Phi(\mathbf{x}_i)\quad(\Phi : \mathbb{R}^d \to \mathbb{R}^N)$$
中,就能很容易地构建一个超平面将数据点作任意聚类。不过由于经 $\Phi$ 映射后的向量是线性无关的,我们无法再像在线性PCA中那样显式地对协方差进行特征分解。
而在核PCA中,我们能够使用任意非平凡的函数 $\Phi$,但无需显式地计算在高维空间中的值,使我们得以使用非常高维的 $\Phi$。为了避免直接在 $\Phi$-空间(即特征空间)中操作,我们可以定义一个 $N\times N$ 的核
$$K = k(\mathbf{x},\mathbf{y}) = (\Phi(\mathbf{x}),\Phi(\mathbf{y})) = \Phi(\mathbf{x})^T\Phi(\mathbf{y})$$
来代表特征空间的内积空间(见格拉姆矩阵)。这一对偶形式使我们能够进行主成分分析,同时又不用直接在 $\Phi$-空间中解协方差矩阵的特征值与特征向量。$K$ 中每一列的 $N$ 个元素代表了转换后的一个数据点与所有 $N$ 个数据点的点积。
由于我们并不在特征空间中进行计算,核PCA方法不直接计算主成分,而是计算数据点在这些主成分上的投影。特征空间中的一点在第k个主成分$V^k$ 上的投影为
$${\mathbf{V}^k }^T\Phi(\mathbf{x})= (\sum_{i=1}^N \mathbf{a_i}^k \Phi(\mathbf{x_i}) )^T \Phi(\mathbf{x})$$
其中 $\Phi(\mathbf{x_i})^T\Phi(\mathbf{x})$ 代表点积,即核 $K$ 中的元素。上式中剩下的部分 $\mathbf{a_i}^k$ 可以通过解特征方程 $$N \lambda\mathbf{a} =K\mathbf{a}$$
得到,其中 $N$ 为数据点的数量,$\lambda$ 与 $\mathbf{a}$ 则分别为 $K$ 的特征值与特征向量。为了归一化 $\mathbf{a}^k$,我们要求 $$1 = (\mathbf{V}^k )^T \mathbf{V}^k$$
值得注意的是,无论是否在原空间中对 $x$ 中心化,我们无法保证数据在特征空间中是中心化的。由于PCA要求对数据中心化,我们可以对 $K$「中心化」: $$K' = K - \mathbf{1_N} K - K \mathbf{1_N} + \mathbf{1_N} K \mathbf{1_N}$$
其中 $\mathbf{1_N}$ 代表一个每个元素值皆为 $1/N$ 的 $N\times N$ 矩阵。于是我们可以使用 $K'$ 进行前述的核PCA计算。
在使用核PCA时,还有一点值得注意。在线性PCA中,我们可以通过特征值的大小对特征向量进行排序,以度量每个主成分所能够解释的数据方差。这对于数据降维十分有用,而这一技巧也可以用在核PCA中。不过,在实践中有时会发现得到所有方差皆相同,这通常是源于错误选择了核的尺度。
大数据集
在实践中,大数据集会使 $K$ 变得很大,从而导致存储问题。一种解决方式是先对数据集聚类,然后再对每一类的均值进行核PCA计算。有时即便使用此种方法仍会导致相对很大的 $K$,此时我们可以只计算 $K$ 中最大的P个特征值及相对应的特征向量。
示例
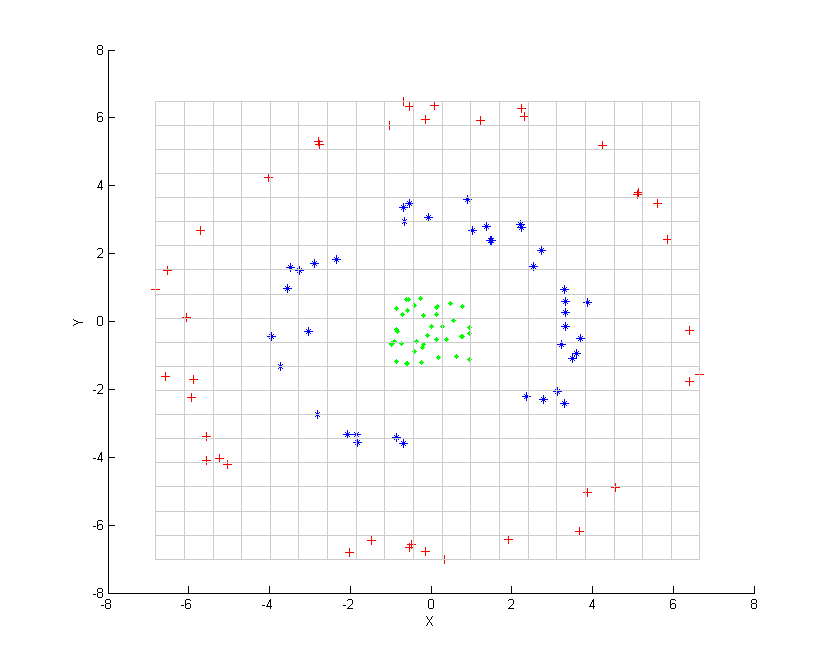
考虑图中所示的三组同心点云,我们试图使用核PCA识别这三组。图中各点的颜色并不是算法的一部分,仅用于展示各组数据点在变换前后的位置。
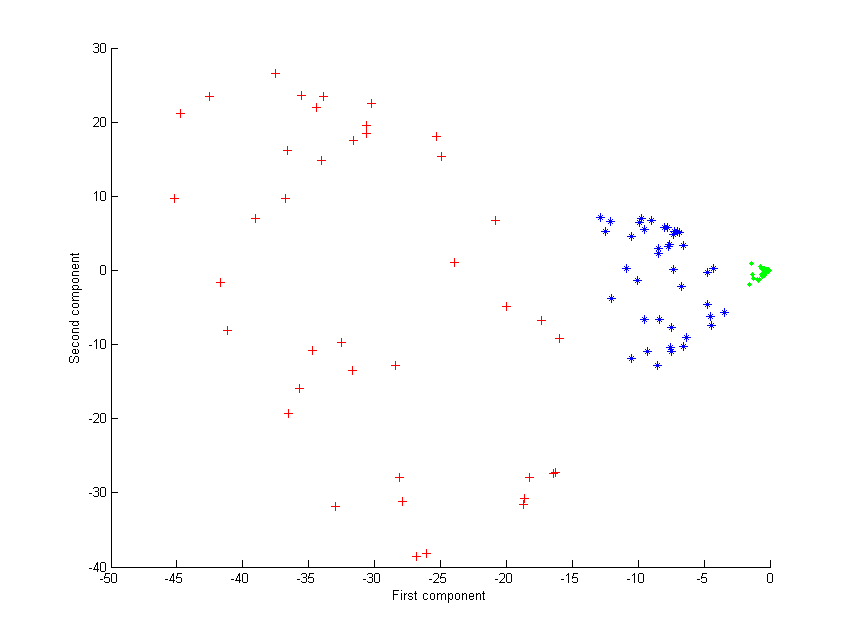
首先,我们使用多项式核 $$k(\boldsymbol{x},\boldsymbol{y}) = (\boldsymbol{x}^\mathrm{T}\boldsymbol{y} + 1)^2$$
进行核PCA处理,得到的结果如第二张图所示。
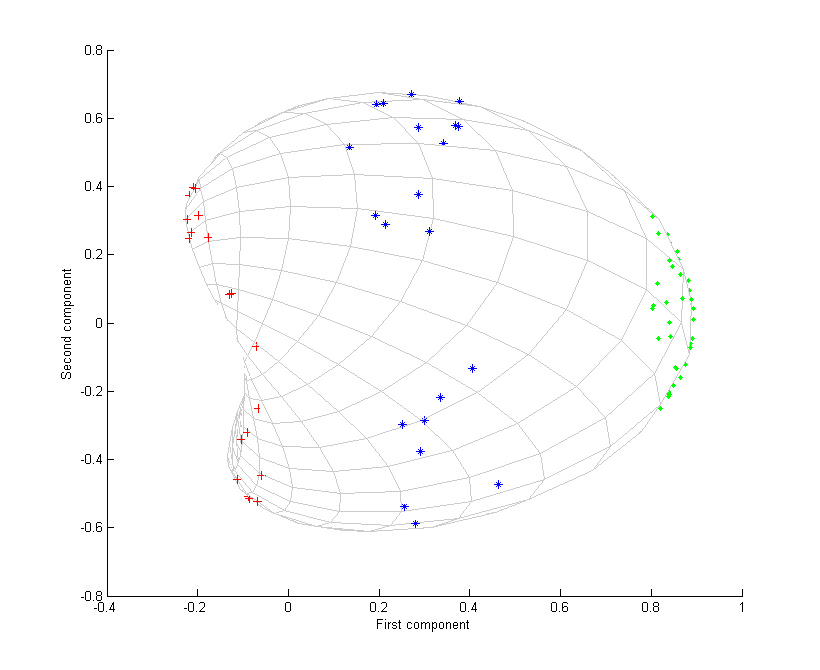
其次,我们再使用高斯核 $$k(\boldsymbol{x},\boldsymbol{y}) = e^\frac{-||\boldsymbol{x} - \boldsymbol{y}||^2 }{2\sigma^2 }.$$
该核是数据接近程度的一种度量,当数据点重合时为1,而当数据点相距无限远时则为0。结果为第三张图所示。
此时我们注意到,仅通过第一主成分就可以区别这三组数据点。而这对于线性PCA而言是不可实现的,因而线性PCA只能在给定维(此处为二维)空间中操作,而此时同心点云是线性不可分的。
应用
核PCA方法还可用于新奇检测(novelty detection)与数据降噪等。