在人工智能技术井喷式发展的今天,机器学习的能力与日俱增,已经能在越来越多的领域赶上、甚至超过人类。那它们能在科学研究上有所建树吗?如果给机器学习算法喂上第谷当年的数据,它们有可能学到开普勒三定律吗?
2016年华盛顿大学的Brunton等人在PNAS上发表的《Discovering governing equations from data by sparse identification of nonlinear dynamical systems》[1]就专门研究了如何从数据中学习动力系统的控制方程。第一作者Brunton 是我硕士时导师的师兄,所以正好关注到了他们的工作。
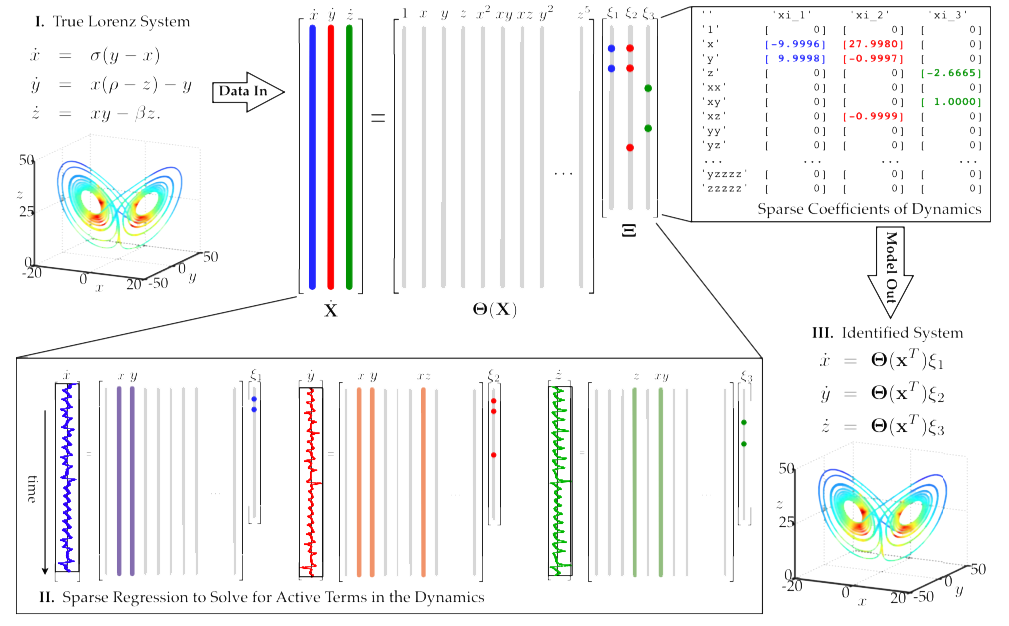
他们这工作是建立在之前基于symbolic regression 的相关工作的基础上的。[2]symbolic regression的问题是computationally expensive,很难scale到高维系统,也容易overfit 。他们提出了一个新的叫SINDy(Sparse Identification of Nonlinear Dynamics)的方法,主要是基于sparse regression 和compressed sensing 的,可以更有效地在高维非线性函数空间中找到真正的控制方程。用这个新方法,他们用数据学习出了洛伦兹系统和圆柱绕流涡旋脱落问题的控制方程。另外,他们还研究了带参的非线性系统的学习问题。
前两天刚结束的AIAA Aviation会议的big data session上,我正好去听了这个研究的另一名作者Nathan Kutz(可能有童鞋在 Coursera上过他教的 data analysis吧)的演讲,说了他们研究的一些最新进展,包括如何用group sparsity 的方法学习带时变参数的系统。有兴趣的童鞋可以去看看他们上个月刚发到arXiv上的《Data-driven identification of parametric partial differential equations》。[3]
Brunton, Proctor, and Kutz (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences, p.201517384. ↩
Rudy et al. (2018) Data-driven identification of parametric partial differential equations. arXiv. ↩